Scaling LLM Test Time Compute

It's October 2024 and the world of large language models (LLMs) is evolving at break-neck speed. Lately, OpenAI has launched its new class of models o1-preview and o1-mini, which are some of the first publicly available models that make use of test-time compute, and they've since topped the leaderboards on a number of benchmarks.

This is exciting, because it seems like there is a new scaling law at play. In addition to training LLMs on more data and for more steps (that's the scaling law we all know and love), we can also throw more compute at a problem at inference time - "letting models think" - and get better performance.

OpenAI 2024

What's behind this progress? It's a combination of many things: new and old techniques from the Reinforcement Learning field being applied to LLM training, bigger and better data sets with human annotations, methods that are easier to scale because remove the need for human annotations, and the list goes on. This blog post should be seen as a snapshot in time, as the field is moving very fast. Consider it a literature review, which doesn't aim to be exhaustive, but gives an overview of interesting papers on test-time compute for LLMs.

Shortcuts:

What is test-time compute?

Test time compute is the amount of compute that is used to generate completions from a language model (LLM) at test or inference time. We might want to scale test time compute for a number of reasons. Most importantly, because we know that LLMs often give wrong answers or hallucinate. Using more compute at inference time has the potential to improve the accuracy or quality of responses, particularly for difficult problems. But there are also other reasons like reducing the size of a model so that it can fit on smaller devices, while maintaining the same level of performance.

A really great paper to start is this one by Snell et al. (2024) [6] which unifies different approaches of test time compute and runs extensive experiments to determine a compute-optimal scaling strategy. Broadly speaking there are two main ways to improve the quality of LLM completions:

At the input level: Modify the prompt in order to get better completions. In other words, we modify the proposal distribution, i.e. the distribution from which different completions are sampled
At the output level: Sample multiple candidate completions and pick the best one or modify them in some way

Viewed through this lense, the question of what exactly we are scaling at test time is broken down into a Proposer and a Verifier. The Proposer is an LLM that generates multiple candidate completions and the Verifier is another model that scores each one and picks the best.

Improve inference by modifying the proposal distribution

Using off-the-shelf LLMs

Methods that fall into this category don't require any fine-tuning of the LLM, they just work with off-the-shelf models. Most of LLM practitioners have probably put a "Take a deep breath and think through it step by step" at the end of their prompt and seen that it helps. I certainly have, and it's been a simple hack to get a bit of extra performance. Alternatively, just breaking up your prompt into smaller parts or asking the LLM to revise its answer can also help. Creating Chain-Of-Thought prompts is another way to guide the LLM to think through a problem step by step: letting it generate intermediate completions sequentially and then using them as input for the next step.

There is a lot of literature on this topic. For example, Saunders et al. (2022) [4] introduce the concept of self-critique which means that

a model generates an answer to a question
it then a model generates a critique of that answer
and both answer and critique are given again to the model to generate a refined answer

Perhaps surprisingly, this method leads to better performance for sufficiently large models. The author argue that this is because it is easier to spot errors in an answer than to avoid them in the first place, which sounds plausible to me!

Madaan et al. (2023) [3] take a very similar approach, and let the model provide feedback and refine its own completions iteratively until a stopping criterion is met.

Madaan et al. 2023

Fine-tuning LLMs

While using off-the-shelf LLMs is nice because it allows anyone to use these techniques, even if they just have access to closed-source models behind APIs, fine-tuning an LLMs to refine their answers can lead to better performance. Zelikman et al. (2022) [11] describe a RL-based approach called STaR, which stands for Self-Taught Reasoner, to bootstrap the ability to generate high-quality rationales.

It's a really cool idea. The authors start off with a base LLM $M$ (they use GPT-J) and an initial training data set of questions and answers pairs. Then they repeat an iterative process until performance plateaus. At each iteration $i$ :

let the LLM from the previous step, $M_{i-1}$ $M_{i - 1}$ (unless it's the first iteration, in which case they use $M$ $M$ ), generate an answer and the rationale for the answer for each question
- if the answer is correct, add this (question, answer, rationale) triplet to the fine-tuning data set
- if the answer is incorrect, give it a hint (the correct answer) and let it generate the rationale for the correct answer. Then add this (question, correct answer, rationale) triplet to the fine-tuning data set
fine-tune the original LLM $M$ on this new fine-tuning data set resulting in a new model $M_{i}$

Note that at each iteration $i$ they fine-tune the original model $M$ from scratch on the fine-tuning data set. So they're not fine-tuning the same model over and over again to avoid overfitting.

This idea of bootstrapping a fine-tuning data set of essentially synthetic training examples (i.e. not human-generated) is something that I cover in more detail in my blog post on synthetic data.

Zelikman et al. 2022

Another example is ReST $^{EM}$ [5], Reinforced Self-Training motivated by the Expectation-Maximization (EM) framework. The approach is not too dissimilar to STaR. The authors repeat the following steps until convergence on the validation set:

Generate many data points using the current model, i.e. let the current model generate completions for a set of questions
Score each of the completions using a binary reward function
Fine-tune the base LLM (PaLM) on the reward-weighted data points

One difference to STaR is that while in STaR only one model-generated solution per question is used, in ReST $^{EM}$ multiple completions can be generated and weighted by the reward function. ReST $^{EM}$ also doesn't use the rationalization step that STaR uses, in which the model generates a rationale for questions on which it got the answer wrong initially. The authors argue that this leads to false positive solutions, i.e. correct answers but incorrect reasoning.

RISE[7], Recursive Introspection for Self-Improvement, is an approach of fine-tuning an LLM to improve its responses sequentially. In a nutshell, the authors turn single-turn problems (i.e. generating the answer to a question in one go) into a multi-turn Markov Decision Process (MDP) in which:

the LLM is a policy $\pi_{\theta}(\cdot|[\mathbf{x}, \mathbf{\^{y}}_{1:t}, p_{1:t}])$ which given a problem $\mathbf{x}$ , previous model attempts to solve the problem $\mathbf{\^{y}}_{1:t}$ (i.e. previous completions) and auxiliary instructions $p_{1:t}$ (e.g. instructions to refine the answer or other feedback), attempts to solve the problem with a new completion. The Self-Refine model[3] mentioned above can also be seen as a special case of this approach, in which only the prompts $p$ are optimized, but not the model parameters $\theta$ .
an action $a$ is a model completion, state $s$ is a concatenation of the previous state, $a$ and an additional fixed prompt $f$ that asks the model to introspect
$r(\mathbf{s}, \mathbf{a})$ is a reward function that scores the completion $a$ given the state $s$ and is either 1 or 0 depending on whether the current completion is correct or not

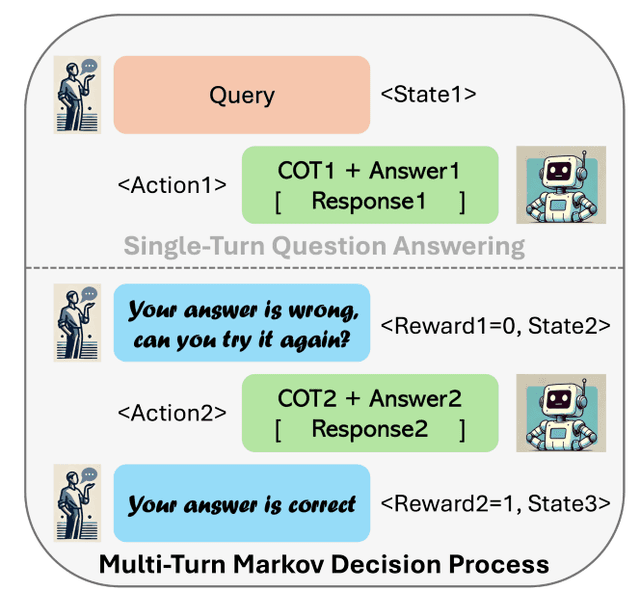Qu et al. 2024

Given the MDP formulation, the authors create a fine-tuning data set, by going through each problem $x_{i}$ and - let the current model $k$ generate multiple sequential attempts to solve the problem $\mathbf{y}^{i}_{t}$ - observe feedback $f^{i}_{t}$ and reward $r(\mathbf{s}^{i}_{t}, \mathbf{y}^{i} _{t})$ for each completion - obtain an improved completion from either a strong teacher model (distillation) or from itself (self-distillation)

It's then possible to fine-tune an LLM on this data and make it learn to recursively detect and correct its own errors in subsequent iterations. Like in STaR and ReST $^{EM}$ , the authors fine-tune the base LLM at each iteration, instead of fine-tuning the same model over and over.

At inference time, the authors the model generate multiple completions and let it revise them sequentially. In the end, a marority vote is used to pick the final completion.

Qu et al. 2024

If you look closely, the process of iteratively refining completions by feeding previous completions and feedback/reasoning back into the model is similar to the approach OpenAI uses in their o1 models.

OpenAI 2024

Improve inference by optimizing the verifier

As mentioned above, the Verifier is a way of selecting the best completion from the proposal distribution. Probably the simplest form of achieving this is Best-of-N sampling, a.k.a. rejection sampling. The basic idea is that instead of just letting the Proposer generate a single completion, we let it generate $N$ completions and then pick the best one.

How do we pick the best one? That's where reward models come in.

Outcome-Supervised Reward Model (ORM)

OpenAI showed in 2021 that it is possible to use an Outcome-Supervised Reward Model (ORM) to improve the performance of LLMs on reasoning tasks like solving math problems.[1] Outcome-supervised essentially means that we let the LLM generate a completion and then evaluate the completion in its entirety with a reward model. This is in contrast to a Process-Supervised Reward Model (PRM), which evaluates intermediary steps of the completion (see below).

Together with the paper, the authors also released a dataset called GSM8K, consisting of 8.5K grade school math problems (7.5K training and 1K test problems) and step-by-step natural language solutions.

The way they train the reward model is as follows:

Train a generator LLM on the training data (i.e. given a math problem, generate a solution)
Use the generator to create 100 completions for each problem in the training data
Hand label each completion as correct or incorrect based on the solution (i.e. just on the outcome, not on the steps taken to get there)
Train a reward model on the questions, completions and labels

At test time the generator and reward model are used like this:

Let the generator create 100 completions for a problem
Use the reward model to score them all and pick the best one

The generator and reward model are both GPT3 models with either 8B or 175B parameters. So it's easy to imagine that this is a very compute-intensive process compared to just generating a single completion.

The results are impressive: as the test performance with Best-of-100 sampling using the reward model (they call it verifier) exceeds the performance of a finetuned baseline by a substantial margin when using a sufficiently large training set.

Also note that when using the ORM approach, the 6B model outperforms the 175B non-ORM model. So while you have to produce multiple completions for each problem, you can get away with a 30x smaller model and achieve the same level of accuracy.

Cobbe et al. 2021

Process-Supervised Reward Models (PRM)

While ORMs evaluate the full generation of an LLM, Process-Supervised Reward Models (PRM) evaluate the generation step-by-step.

Using the same GSM8K as above, DeepMind researchers[8] did a side-by-side comparison of ORMs and PRMs in 2022. In order to train the PRM, which requires human feedback on intermediary steps, they use human annotators to obtain binary labels for each step of each completion in the GSM8K dataset.

Their Best-of-N sampling is a bit different. They generate 96 completions at test time, but instead of just picking the highest scoring one, they weigh each answer candidate by the scores given by the PRM and then pick the one with the highest total weight.

The results from this study are that, judged by the final-answer error rate, ORM and PRM perform similarly. However, the authors show that the trace error rate (i.e. the correctness of reasoning steps) can be significantly improved by using process-based feedback.

Back at OpenAI, researchers conducted their own ORM vs. PRM comparison in 2023.[2] The main result is that when using a more capable base model (GPT4 instead of Chinchilla), and trained on more human feedback, PRM can significantly outperform ORM also on final-answer error rate.

The data set is different. Since the authors wanted to train on more data, they took the MATH data set as a starting point, which consists of 12,500 math problems with step-by-step solutions, and which is also more challenging than GSM8K. To obtain supervision data for the reward model, they use the generator model (GPT4, with a little bit of math-specific finetuning) to create step-by-step solutions for each problem in the MATH data set. Then they use human annotators to label each completion as positive, negative or neutral. Overall this results in a data set of 800K step-by-step labels, which is why this data set is called PRM800K.

The PRM is trained to predict a single token at the end of each step indicating whether the step is correct or not. This allows the training to happen as a usual language modelling task. At test time, a single pass of the completion is enough to generate all the step-wise feedback. The correctness of the overall answer is then computed as the product of the correctness probabilities of all steps.

In this paper, the authors again use plain Best-of-N sampling to evaluate the reward model. Here is a comparison of ORM and PRM, showing the superior performance of PRM.

Lightman et al. 2023

At first glance, the result seem to contradict the 2022 DeepMind paper.[8] However, the authors argue that the difference in performance is due to the scale of the human supervision data.

How do you scale this further? Wang et al. (2023)[9] show that it is possible to obtain an annotated data set for PRM training without human supervision. Given a data set of math problems and step-by-step solutions (however, where the steps are not annotated), they use an LLM to generate multiple reasoning paths leading to an answer. The ones leading to the correct answer, the reasoning steps get a higher correctness score than the ones leading to the wrong answer. While the resulting data set is of high quality, the authors note that this approach can lead to false positives if you generate too many examples.

Going beyond Best-of-N sampling

Instead of simply picking the highest scoring completion, using a PRM allows for more sophisticated ways of selecting the best completion such as tree search. For example Yao et al.[10] introduce the concept of a Tree of Thoughts which is a structured way to guide the LLM through a problem. Using a tree-based structure instead of a linear chain of thoughts, the LLM is able to explore different paths, backgrack and lookahead, which leads to better performance on certain reasoning tasks.

Compute-optimal scaling

Back to the paper I mentioned in the beginning, Snell et al. (2024)[6] recently showed that using more test-time compute can be more effective than scaling model size. Following their unified Proposer/Verifier-framework, they show that the different test-time compute strategies have different effectiveness depending on the difficulty of the problem. Therefore, they propose a compute-optimal scaling strategy that is adaptively applied per prompt. Like in Lightman et al. (2023),[2] they use a model to estimate the difficulty of a problem.

When it comes to the Verifier, the authors use a PRM that is trained without human supervision like in Wang et al. (2023).[9] The PRM can be used at test time to score each step of a completion in 3 different ways:

Best-of-N weighting: simply sampling N answers and selecting the one that gets the highest final score by the PRM
Beam search: similar to Yao et al.[10] conduct a beam search over the PRMs per-step scores
Lookahead search: similar to beam-search, but instead of just looking at the next step, do a k-step lookahead and use the PRMs score of that step for deciding which paths to take

The results show that the effectiveness of the different strategies depends on the compute budget and the difficulty of the problem.

Compute Budget: Beam search is most effective for low-compute budgets, while Best-of-N is most effective for high-compute budgets, and Lookahead search is never the best choice.
Difficulty: on easy questions Best-of-N the best strategy, while on more difficult questions Beam search is more effective.

As for the Proposer, the authors use an approach similar to RISE[7] with some differences:

generating revision data: for efficiency reasons, the authors sample 64 responses in parallel at high temperature and then pair up to four incorrect ones with one correct one to construct a multi-turn training example.
using revisions at inference time: the model was trained with only incorrect answers in context (and the last one correct), but at inference time there might be correct answers in context. So the model might accidentally turn some correct answers into incorrect ones - this happens around 38% of the time. To mitigate this, the authors use sequential majority voting or verifier-based selection to select the most correct answer.

Modifying the proposal distribution like above works well. As you can see below, increasing the number of generated completions at test time leads to better performance up to a certain point.

Snell et al. 2024

Since it's possible to sample multiple revisions in parallel or sequentially at test time, the authors also analyse which way leads to better performance. The results show that sampling sequentially performs better.

Snell et al. 2024

However, there might be benefit in using both approaches as they might lead to different answers. Sampling in parallel, you might effectively do more of a global search, so you end up trying out different approaches. Compared to that, when sampling sequentially the model is more likely to go down a certain reasoning path. The authors show that for simple problems, sampling sequentially is more effective, while for more difficult problems, there is actually an optimal ratio of parallel to sequential sampling.

Putting everything together, it's possible to combine the Proposer and Verifier in a way that is compute-optimal for a given problem. The authors show that to some extent, test-time compute can be traded off with pretraining-compute. That is, you can use smaller models or models that haven't been pre-trained for as long, and boost their performance using the test-time strategies described above. However, this is only true for easy and medium problems. For hard problems the authors find that pre-training is likely to be more effective.

Conclusion

As I mentioned in the beginning, the field is moving very fast right now. There are at least 3 papers on my reading list that were published over the last 2 weeks

Adaptive Inference-Time Compute:LLMs Can Predict if They Can Do Better, Even Mid-Generation [paper]
Rewarding Progress: Scaling Automated Process Verifiers for LLM Reasoning [paper]
VerifierQ: Enhancing LLM Test Time Compute with Q-Learning-based Verifiers [paper]

I believe the direction in which the field is headed is clear: LLMs will become more reliable and more capable of solving complex problems using "chains of thought". This will have practical implications for practitioners and start up founders too. If your current moat is a clever way of stringing together specific prompts to enable use-cases that simple one-turn (i.e. one completion) completions can't solve, you might want to start thinking about how to adapt to this new world. Telling LLMs to "think through it step by step" or explicitly setting out the steps required to solve a problem might not be necessary anymore for many use cases.

If one thing is certain, it's that these are just the early innings of scaling test time compute. So now is the best time to read up on it and stay up to date with the cutting edge.

There has been a lot of talk lately about LLMs hitting a wall in terms of performance. This seems to be mainly in relation to pre-training, and limitations to how much that can be scaled. I'll close this blog post on a positive note, with a short excerpt of a talk by Noam Brown (Research Scientist at OpenAI) who talks about how we can hopefully push LLM performance further using inference compute. Fingers crossed.

Loading Tweet Video...

If you liked this article, you might also enjoy my blog post on generating synthetic data for LLMs post-training.

I hope you found this article helpful - see you next time!

References

[1] K. Cobbe, V. Kosaraju, M. Bavarian, M. Chen, H. Jun, L. Kaiser, M. Plappert, J. Tworek, J. Hilton, R. Nakano, C. Hesse, and J. Schulman. Training verifiers to solve math word problems, 2021. [paper]

[2] H. Lightman, V. Kosaraju, Y. Burda, H. Edwards, B. Baker, T. Lee, J. Leike, J. Schulman, I. Sutskever, and K. Cobbe. Let's verify step by step, 2023. [paper]

[3] A. Madaan, N. Tandon, P. Gupta, S. Hallinan, L. Gao, S. Wiegreffe, U. Alon, N. Dziri, S. Prabhumoye, Y. Yang, S. Gupta, B. P. Majumder, K. Hermann, S. Welleck, A. Yazdanbakhsh, and P. Clark. Selfrefine: Iterative refinement with self-feedback, 2023. [paper]

[4] W. Saunders, C. Yeh, J. Wu, S. Bills, L. Ouyang, J. Ward, and J. Leike. Self-critiquing models for assisting human evaluators, 2022. [paper]

[5] A. Singh, J. D. Co-Reyes, R. Agarwal, A. Anand, P. Patil, X. Garcia, P. J. Liu, J. Harrison, J. Lee, K. Xu, A. Parisi, A. Kumar, A. Alemi, A. Rizkowsky, A. Nova, B. Adlam, B. Bohnet, G. Elsayed, H. Sedghi, I. Mordatch, I. Simpson, I. Gur, J. Snoek, J. Pennington, J. Hron, K. Kenealy, K. Swersky, K. Mahajan, L. Culp, L. Xiao, M. L. Bileschi, N. Constant, R. Novak, R. Liu, T. Warkentin, Y. Qian, Y. Bansal, E. Dyer, B. Neyshabur, J. Sohl-Dickstein, and N. Fiedel. Beyond human data: Scaling self-training for problem-solving with language models, 2024. [paper]

[6] C. Snell, J. Lee, K. Xu, A. Kumar. Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters, 2024. [paper]

[7] Y. Qu, T. Zhang, N. Garg, and A. Kumar. Recursive introspection: Teaching foundation models how to self-improve. 2024. [paper]

[8] J. Uesato, N. Kushman, R. Kumar, F. Song, N. Siegel, L. Wang, A. Creswell, G. Irving, and I. Higgins. Solving math word problems with process-and outcome-based feedback, 2022. [paper]

[9] P. Wang, L. Li, Z. Shao, R. X. Xu, D. Dai, Y. Li, D. Chen, Y. Wu, and Z. Sui. Math-shepherd: Verify and reinforce llms step-by-step without human annotations, 2023. [paper]

[10] S. Yao, D. Yu, J. Zhao, I. Shafran, T. L. Griffiths, Y. Cao, and K. Narasimhan. Tree of thoughts: Deliberate problem solving with large language models, 2023. [paper]

[11] E. Zelikman, Y. Wu, J. Mu, N. D. Goodman. STaR: Self-Taught Reasoner Bootstrapping Reasoning With Reasoning, 2022 [paper]